Integer – A whole number. Not a fraction.
Pitch – A specific note in a specific octave.
Pitch Class – A specific note, but can be in any octave.

When you get to Theory IV you will spend a lot of time talking about pitches and notes as numbers instead of letter names and accidentals. This is because for about 100 years, the musical vocabulary of some music is so far away from tonal music, that it is easier to describe and analyze with integers.

Since there are 12 different notes on a keyboard in any given octave, it is easiest to visualize our use of integers on a diagram similar to a clockface or a circle of fifths. (It ends up being a circle of half steps.)

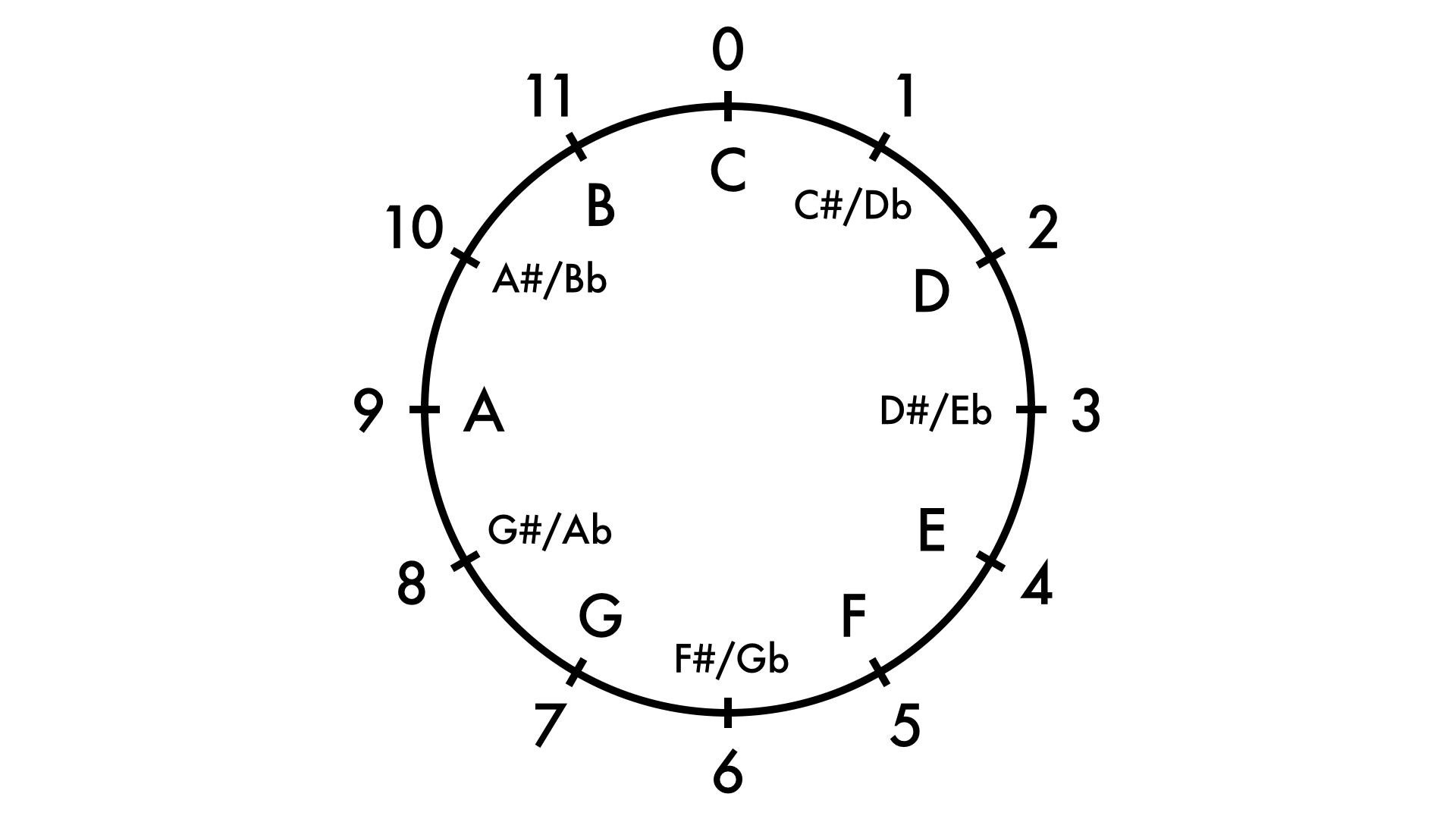
In this system, C equals 0, C sharp and D flat both equal 1, and so on through B equalling 11. We use 0 to make the large amounts of arithmetic work out smoothly. We often measure distances between notes (intervals) rather than just the number of notes. So I find it helpful to think of the pitch-class integers as places of measurement on a circular ruler, like in the diagram.

The integers and circle end up being very useful. Say you want to know the number of half steps between B flat and E. If you know that B flat is 10 and E is 4, you just subtract. 10 – 4 = 6 half steps. So, if you are used to half-step counting, learning these integers will help you speed up your process, and prepare you for a class in your future.

But notice that we can go either way around the circle. And with intervals, we usually need know which way, because the order of the pitches matters. Either note can be on top. So if you are measuring from the bottom up, go clockwise. If you are measuring top down, go counterclockwise. For instance, C# up to E is 4 – 1 = 3 half steps. But C down to E is 13 – 4 = 9 half steps. Notice that I had to add 12 to 1 to make 13 for the math to work. This is the same kind of thinking you do when you figure out how many hours there are between 8 am and 4pm, and then 4pm and 8am.